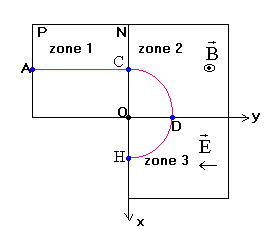
| Chimie: Exercice1: 1)Donner les définitions électroniques d'un oxydant et d'un réducteur. 2)Le fer peut donner naissance à deux types d'ions, en solution aqueuse: *L'ion ferreux de formule: Fe2+. *L'ion ferrique de formule: Fe3+. a-Ecrire les demi-équations des couples faisant intervenir Fe; Fe2+et Fe3+. b-Montrer que l'ion ferreux peut jouer, selon le cas, le rôle d'un oxydant ou d'un réducteur. c-On observe que Fe2+dans le couple Fe2+/Fe est moins oxydant que Fe3+dans le couple Fe3+/Fe2+. Ecrire l'équation-bilan traduisant la réaction entre ces deux couples. Expliquer pourquoi, on met souvent, au laboratoire; du fer Fe au fond des flacons des solutions aqueuses de fer II pour les conserver. 3)On dispose des espèces chimiques suivantes: Cr3+ ; CH4O ; Cr2O72- ; CH2O2. a-Former des couples oxydant-réducteur en utilisant ces espèces en milieu acide, et écrire, pour chaque couple, la demi-équation correspondante. b-Ecrire l'équation globale d'oxydo-réduction sachant que Cr3+est moins réducteur que CH4O. Exercice 2: On donne Fe=56g.mol-1. On verse une solution d'acide chlorhydrique dans deux tubes à essais contenant l'un des copeaux de cuivre et l'autre de la limaille de fer. 1)a-La solution d'acide chlorhydrique n'agit pas sur les copeaux de cuivre alors qu'elle attaque la limaille de fer. Expliquer pourquoi. b-Ecrire alors l'équation de la réaction. 2)Une masse de 0,2g de limaille de fer est attaquée par 100mL d'une solution d'acide chlorhydrique de concentration molaire 10-2mol.L-1. a-Quelle est la masse de la limaille de fer restante à fin de la réaction? b-Le mélange obtenu est filtré. Le filtrat constitue une solution (S) de volume 100mL. Déterminer sa concentration molaire C des ions Fe2+. Physique: Exercice 1: Dans cette partie, on négligera le poids de particules chargées. Un faisceau de particules de charge q=1,6.10-19 C et de masse m=1,6.10-27Kg pénètre par le trou A d'un accélérateur (zone 1) avec une vitesse nulle. Ces particules chargées sont accélérées sous l'action d'une d.d.p positive U=UPN=200V établie entre les plaques parallèles et verticales P et N. Elles parviennent au trou C avec une vitesse de valeur vC. 1)Etablir l'expression de vC en fonction de q; m et U. Faire l'application numérique. 2)Le faisceau pénètre ensuite dans une région où règne un champ magnétique uniforme (zone 2) dans laquelle il décrit un quart de cercle de rayon R=20cm avant de passer à travers le trou D. a-Etablir l'expression de la valeur du champ magnétique en fonction de m; q; R; vC puis en fonction de U; R et vC. Faire le calcul numérique. b-Donner les caractéristiques (direction et valeur) du vecteur vitesse des particules à la traversée du trou D. 3)Le faisceau de particules pénètre enfin dans une région dans laquelle règne un champ électrostatique uniforme parallèle à l'axe Oy (zone 3). a-Etablir les équations horaires du mouvement projeté sur les axes Ox et Oy. b-En déduire l'équation et la nature de la trajectoire. c-Sachant que le faisceau de particules sort par le trou H situé à la distance R=20cm du point O. Exprimer dans cette condition la valeur du champ électrostatique en fonction de m; q; vC et R puis en fonction de U et R. Faire l'application numérique. |