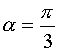Devoir 401:Quatrièmes années Math,Sciences expérimentales et Technique.

Chimie: Les deux exercices 1 et 2 sont indépendants.
Exercice 1:
La dissociation du pentachlorure de phosphore aboutit à un équilibre chimique schématisé par l'équation :

La dissociation (sens direct) est exothermique.
1)Prévoir, en le justifiant ; le sens du déplacement de l'équilibre précédent si :
a-On comprime le mélange gazeux.
b-On augmente sa température.
c-On élimine le trichlorure de phosphore.
2)Une mole de pentachlorure de phosphore est placée dans un récipient de volume V=2L à la température T. L'équilibre s'établit lorsque 36% du PCl₅initial se sont dissociés.
a- Déterminer la composition molaire du mélange gazeux à l'équilibre.
b- Calculer la constante d'équilibre K_crelative aux concentrations molaires à la température T.
3)La température est maintenue constante, on diminue brusquement le volume
jusqu'au V'=1,5L.
a- La composition molaire précédente subira-t-elle un changement ?
Si oui dans quel sens l'équilibre va-t-il se déplacer ? Justifier.
b- Déterminer la nouvelle composition du mélange à l'équilibre.
c- Chercher la nouvelle valeur du taux de dissociation de PCl₅.
Montrer que ce résultat est compatible avec les prévisions qualitatives que l'on
pouvait faire.
Exercice 2:
On effectue l'oxydation des ions iodure I^- par les ions peroxodisulfate S₂O₈⁼en
faisant réagir de l'iodure de potassium sur du peroxodisulfate de potassium.
Le mélange initialement incolore devient jaunâtre par suite de l'apparition progressive
du diiode I₂.
1)Ecrire l'équation bilan de la réaction qui se produit.
2)Le mélange étant maintenu à 20°C. Les molarités initiales des ions réagissant
sont: [I^-]_o=4.10^-2mol.L^-1 et [S₂O₈⁼]_o=2.10^-2mol.L^-1.Des prélèvements des volumes négligeables par rapport au volume total du mélange, permettent à intervalles de
temps constants, de doser le diiode présent.
On obtient les valeurs suivantes :

Temps t (min)	10	20	30	40	50	60
[I₂].10³mol.L^-1	1,37	2,42	3,26	4	4,53	4,95

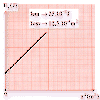
a- Tracer convenablement la courbe [I₂]=f(t). Déterminer [I^-]à t=35min.
b- Déterminer graphiquement la vitesse instantanée du diiode aux dates t₁=0min et t₂=40min. Expliquer la variation de cette vitesse.
3)On recommence l'expérience dans des conditions différentes et dans chaque cas
on dose le diiode formé au bout d'un intervalle de temps égal à 10min.
On obtient les résultats suivants :

[S₂O₈⁼]_o.10²mol.L^-1	[I^-].10²mol.L^-1	Température		[I₂].10³mol.L^-1
1	2	40°C		3,4
1	2	20°C		0,53
2	4	40°C		5,5
1	2	20°C	+ Fe²⁺	3,05

a- Comparer les conditions expérimentales précédentes.
b- Calculer la vitesse moyenne de réaction dans l'intervalle de temps [0 ; 10min] dans chacun de ces cas.
En déduire l'influence des divers facteurs pouvant modifier la vitesse de réaction.
Physique: Les trois exercices sont indépendants. Prendre g=10usi.
Exercice 1:
On considère un parcours ABC sous forme d'arc de cercle de rayon R=1m, situé
dans un plan vertical et de centre O ; le bord A du parcours appartient au même
plan horizontal que le centre O alors que le bord C est tel que l'angle:

Le point B est le point le plus bas de la piste. (Voir figure ci-dessous).

Le plan horizontal contenant le point B sera pris comme niveau d'énergie potentielle nulle. Un solide ponctuel(S) de masse m=100g est libéré sans vitesse initiale au
bord de la piste ABC le long de laquelle il réalise un glissement sans frottement.
1)a- Calculer la valeur de l'énergie mécanique du système: { terre + (S)} à l'instant
       de libération de (S).
   b- La valeur de cette énergie varie-t-elle au cours du temps ? Justifier.
2)a- Indiquer, sans calcul la position où la vitesse de (S) est maximale.
   b- Calculer la vitesse du solide(S)à sa position la plus basse:
       *En utilisant le théorème de variation de l'énergie cinétique.
       *En raisonnant à partir de l'énergie mécanique.
3)Le solide (S), après son départ de A, parvient au point C avec une vitesse nulle à cause de l'existence de frottements.
Calculer la valeur de l'énergie mécanique du système { terre + (S)} au point C.
Déterminer, au bout du déplacement de (S) de A jusqu'au point C, la quantité d'énergie mécanique convertie en chaleur par suite des frottements.
Exercice 2:
Un corps (C) de masse m est accroché à l'extrémité inférieure d'un ressort parfait
de raideur K dont l'autre extrémité est fixe.
Le corps (C) est astreint à se déplacer, sans frottement en translation sur la ligne
de plus grande pente d'un plan incliné d'un angle

par rapport à l'horizontale.
On choisira un axe X'X descendant et parallèle au plan incliné et on prendra comme origine des élongations x le point O : la position d'équilibre du corps (C).
On écarte le corps (C) de sa position d'équilibre d'une distance x_oet à la date t=0s prise comme origine des temps, on l'abandonne sans vitesse initiale.
On prendra comme plan de référence le plan horizontal passant par le point O et
on considérera à ce niveau que l'énergie potentielle de pesanteur est nulle.
1)Etablir l'expression de l'énergie potentielle du système (S)={ terre + (C) + ressort}
à une date t ultérieure en fonction de l'abscisse x du centre d'inertie du corps (C) la raideur K du ressort et de sa déformation a à l'équilibre.
2)a- Exprimer la variation de l'énergie potentielle de (S) au cours du déplacement du corps (S) d'une position (1) d'abscisse x₁ à une position (2) d'abscisse x₂.
b- Faire l'inventaire des forces exercées sur le corps(C)puis exprimer le travail de
ces forces lors de son déplacement de la position (1) à la position (2).
c- Montrer que les résultats précédents vérifient le théorème de la variation de l'énergie potentielle.
3)On donne ci-contre la courbe Ep=f(x²) représentant l'énergie potentielle du
système (S) en fonction du carré de l'élongation x du corps (C) :

a-En se servant de cette courbe et de la question 1) déterminer la raideur K du ressort et sa déformation a lors de l'équilibre du corps (C).
b-En déduire la masse m du corps (C) sachant que:

=30°.
Exercice 3:
On considère un ressort (R) de masse négligeable, à spires non jointives de raideur K=40N.m^-1 et de longueur à vide l₀=30cm. Ce ressort est disposé verticalement,
son extrémité inférieure est fixée à un support horizontal et son extrémité supérieure est liée à un plateau (P) de masse m=50g et restant toujours horizontal.
On place un cylindre ponctuel (C) de même masse m dans une cavité ménagée au centre du plateau (C).
L'ensemble { plateau (P) + cylindre (C) } constitue un solide (S).
On choisira un axe vertical Oz orienté vers le bas, et d'origine le point O : la position d'équilibre de (S) et on suppose que le ressort (R) reste toujours vertical.

1)Chercher la longueur du ressort (R) à l'équilibre de (S).
2)On écarte le solide (S) vers le bas d'une distance égale à 3cm à partir du
point O et on lui communique à la date t=0s une vitesse initiale positive de valeur 0,8m.s^-1.
On suppose que le cylindre reste en contact avec le plateau et on néglige tout phénomène d'amortissement.
a- Etablir l'équation différentielle régissant le mouvement du solide (S).
b- Préciser la nature du mouvement du solide (S) et calculer sa période propre.
Etablir sa loi horaire.
c- Montrer que le cylindre (C) quitte le plateau (P) quand ce dernier atteint une position que l'on précisera par rapport au point O.