| Chimie: Les deux parties I
et II sont indépendantes. Partie I: On considère la réaction de synthèse du trioxyde de soufre: Dans un récipient de volume V=100L, on introduit 1 mole de dioxyde de soufre et 0,5 mole de dioxygène à une température T et une pression P données. 1)a- Montrer qu'au cours de la réaction on a le rapport des concentrations: 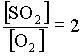 b- Exprimer la constante d'équilibre K en fonction de V et des nombres de moles de O2 et de SO3 à l'équilibre. c- A l'équilibre le nombre total de moles gazeuses est n=1,021 moles. Calculer K. 2) Le mélange précédent est porté à une température T'>T. On constate que pour le nouvel état d'équilibre la constante d'équilibre K' est inférieure à K. a- La synthèse du trioxyde de soufre est-elle endothermique ou exothermique ? Justifier la réponse et énoncer la loi utilisée. b- Quelle est l'influence d'une élévation de la température sur le rendement de la réaction de formation du trioxyde de soufre ? 3) La température étant maintenue constante, quel est l'effet d'une augmentation de la pression sur la composition du mélange à l'équilibre et sur la constante d'équilibre ? Partie II: On donne le pKa de l'acide éthanoique égal à 4,8 et on prendra pKe =14. On prépare une solution aqueuse (S) d'acide éthanoique de concentration molaire initiale C et dont le pH vaut 3. 1)a-Donner l'expression de C en fonction du pH et du pKa de l'acide éthanoique. Calculer C. b-Déterminer le coefficient de dissociation de l'acide éthanoique dans la solution (S). 2)a- Quel volume d'eau faut-il ajouter à 10cm3 de la solution précédente (S) pour obtenir une solution aqueuse (S1) de pH1=3,5 ? b- Quelle masse d'acide éthanoique pur faut-il ajouter à 1L de la solution (S) de pH=3 pour obtenir une solution (S2) de pH2=2,9 en admettant que le volume ne change pas ? On donne : H=1g.mol-1 ; C=12 g.mol-1 et O=16 g.mol-1. 3) On prépare une solution aqueuse (S') d'acide méthanoique (pK'a =3,8) de même concentration molaire C que la solution précédente (S) d'acide éthanoique. Le pH de la solution (S') est-il supérieur ou inférieur à 3 ? Justifier. Physique: Les deux parties A et B sont indépendantes. Partie A: Un pendule élastique horizontal est formé d'un ressort (R) à spires non jointives, de masse négligeable, de raideur K=20N.m-1 dont l'une de ses extrémités est fixe et à l'autre est accroché un solide ponctuel (S) de masse m=50g. La position de (S) est repérée par son abscisse : 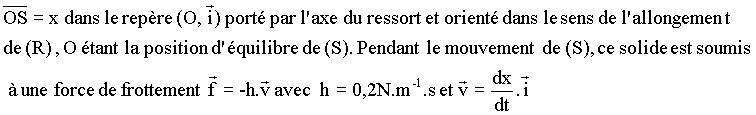 I- On écarte le solide (S) de x0=6cm à partir de O et on l'abandonne sans vitesse initiale à t=0s. Le solide S effectue alors un nombre assez grand d'oscillations d'amplitude décroissante, avec une pseudopériode T pratiquement égale à la période propre T0 de l'oscillateur. 1) Donner l'analogue électrique de l'oscillateur mécanique amorti considéré. Ecrire l'équation différentielle régissant les oscillations de la charge q. En déduire par analogie l'équation différentielle en x. 2)Montrer que l'énergie mécanique totale E du pendule élastique est décroissante. 3)En admettant que le mouvement du solide (S) est pratiquement sinusoïdal pendant la première oscillation et que dE/dt est pratiquement constante dans une durée très petite par rapport à T0, calculer l'énergie dissipée en chaleur par la force de frottement entre t1= T0/4 et t2= T0/4 + T0/20. (Question facultative sur 1 point). 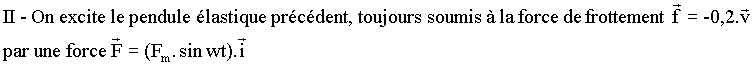 Le solide (S) est alors animé d'un mouvement rectiligne sinusoïdal de même pulsation w que la force excitatrice et d'élongation: 1)a-Donner sans démonstration les expressions de Xm et tgØ. b-En déduire l'expression de l'amplitude Vm de la vitesse du solide (S). 2)a-Rappeler l'expression de l'impédance électrique de l'oscillateur forcé RLC puis exprimer par analogie de l'impédance mécanique Zméc du pendule élastique. b-Retrouver l'expression de Zméc à partir de sa définition et de l'expression de Vm. 3)On donne Xm=4cm et w=16rad.s-1. Calculer Vm ; Fm ; Ø ; Zméc. Partie B: Une tension alternative sinusoïdale: (u en V et t en s) alimente un circuit formé par une bobine (b) d'inductance L=0,25 H et de résistance interne r=10 1)Etablir l'équation différentielle régissant les variations de l'intensité instantanée i du courant dans le circuit RLC au cours du temps. 2)La solution de l'équation différentielle précédente est: a-Rappeler sans démonstration l'expression de I en fonction des données du problème et calculer sa valeur numérique. b-Faire la construction de Fresnel correspondante en prenant l'échelle 1cm c-Déduire du diagramme de Fresnel : * L'amplitude Ubm de la tension aux bornes de la bobine. **Le déphasage entre la tension d'alimentation u et l'intensité i du courant. ***Le déphasage entre la tension ub aux bornes de la bobine (b) et l'intensité i. 3)La tension uR aux bornes du résistor R et la tension u aux bornes de l'ensemble sont visualisées simultanément sur un oscillographe à double voie, respectivement à la sensibilité verticale de 5V.cm-1 et 10V.cm-1 et le balayage horizontal de 2,5ms.cm-1. On obtient sur l'écran de l'oscillographe cathodique deux sinusoïdes synchrones et décalées l'une par rapport à l'autre. L'axe de temps étant centré : a-Par combien de cm représente-t-on l'amplitude de chacune de ces sinusoïdes? b-Déterminer la distance minimale sur l'axe de temps entre les passages de ces deux sinusoïdes par zéro dans le même sens en précisant laquelle de ses deux courbes est à droite par rapport à l'autre ? c-Dans quel sens et de combien doit-on faire varier la fréquence de la tension u pour obtenir sur l'écran de l'oscillographe deux sinusoïdes en concordance de phase? 4) La condition de la question 3)c- étant réalisée: a-Déterminer l'intensité efficace I0 du courant à travers le circuit. b-Calculer les tensions efficaces Ub0 et Uc0 respectivement aux bornes de la bobine (b) et le condensateur. c-Chercher le coefficient de surtension (ou de qualité) du circuit. |