| Chimie: Les deux exercices
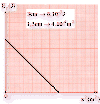
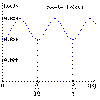
1 et 2 sont indépendants. Exercice 1 : La synthèse du bromure de nitrosyle NOBr est schématisée par l'équation : Tous les corps mis en jeu sont à l'état gazeux. 1)Dans une enceinte de volume 15L, on introduit 0,6mol de monoxyde d'azote et 0,3mol de dibrome. A la température T1=700°C, le système aboutit à un équilibre chimique tel que le nombre total de moles gazeuses serait égal à 0,85. a- Chercher la composition molaire du mélange gazeux à l'équilibre. b- Calculer la constante d'équilibre Kc1 relative aux concentrations molaires à T1. 2)A la température T2=800°C, un nouvel état d'équilibre s'établit et la nouvelle composition du mélange gazeux est la suivante : 0,32mol de monoxyde d'azote ; 0,16mol de dibrome et 0,28mol du bromure de nitrosyle. Sachant que le volume et la pression sont maintenus constants : a- Dans quel sens a évolué le système chimique précédent pour aboutir à ce nouvel état d'équilibre ? b- Préciser le caractère énergétique de la synthèse de NOBr ? Justifier. c- Chercher la valeur de la constante d'équilibre Kc2 à la température T2 . 3)Le volume et la pression sont maintenus toujours constants. On considère maintenant un nouveau mélange formé de 4.10-1mol de NO ; 2.10-1mol de Br2 et 4.10-1mol de NOBr à la température T2=800°C. a- Ce système chimique est-il en état d'équilibre ? Justifier. b- Si non, dans quel sens va-t-il évoluer au cours du temps ? Exercice 2 : Dans un récipient fermé de volume V=20L, initialement vide ; on introduit n0 mole de tétraoxyde de diazote à une température T. Lorsque l'équilibre chimique : s'établit, 20% du tétraoxyde de diazote initial se sont dissociés. 1)Exprimer la constante d'équilibre Kc1 à T en fonction de n0 et V. 2)A l'équilibre la somme des nombres de moles de N2O4 et NO2 est égal à 1,2mol. Déterminer Kc1. 3)Dans le même récipient de volume V=20L, initialement vide ; on introduit 1mol de N2O4 et 2mol de NO2 à une température T'. La constante d'équilibre est égale Kc2=0,1 à cette température. a-Déterminer la composition du mélange lorsqu'on atteint l'équilibre chimique. b-La réaction de dissociation de N2O4 est endothermique. Comparer T et T'. Justifier. Physique: Les deux exercices 1 et 2 sont indépendants. Prendre g=10usi. Exercice 1 : Un solide ponctuel (C) de masse m est relié à l'extrémité inférieure d'un ressort parfait (R) de raideur K dont l'autre extrémité est fixe. L'ensemble est situé suivant la ligne de plus grande pente d'un plan incliné faisant un angle Ø avec l'horizontale. On néglige tous les frottements. On choisira un axe x'x descendant et parallèle au plan incliné et on prendra comme, origine des élongations, la position d'équilibre O du solide (C). A l'équilibre le ressort (R) s'allonge de a. 1)Etablir la relation entre K ; a ; m ; g et Ø. 2)On écarte le solide (C) de sa position d'équilibre vers le bas d'une distance x0 et on l'abandonne à lui-même à la date t=0s. a-Par application de la relation fondamentale de la dynamique au solide (C) établir l'équation différentielle régissant son mouvement. b-Préciser la nature de ce mouvement et exprimer sa fréquence propre en fonction de K et m. 3)A une date t ultérieure, l'élongation du solide (C) est x et sa vitesse est v=dx/dt. Le plan de référence pour l'énergie potentielle de pesanteur passe par le point O. a-Etablir l'expression de l'énergie potentielle Ep du système déformable: (S)={ Solide (C) + Terre + ressort (R)} en fonction de x ; K et a. b-Montrer que l'énergie mécanique totale E du système (S) est constante et donner son expression en fonction de K ; x0 et a. c-Etablir l'expression de l'énergie cinétique Ec de (C) en fonction de x ; K et x0. 4)Une étude expérimentale a permis de tracer les courbes : Ec=f(x2) et Ep=g(t). (Voir figures ci-dessous): |
|
| a- En exploitant ces deux courbes et en se servant de la
question 3) : *Déterminer la valeur maximale de l'énergie cinétique de( C), la valeur minimale de l'énergie potentielle de (S) et la valeur de son énergie mécanique. *Déterminer l'allongement a du ressort (R) à l'équilibre, sa raideur K ainsi que l'élongation x0 du solide(C)à la date t=0s. b-Montrer que la pulsation propre du mouvement du solide (C) est w0 =10rad.s-1. c-En déduire la masse m de (C) et l'angle Ø entre le plan incliné et l'horizontale. d-Etablir la loi horaire décrivant le mouvement du solide (C). e-Déterminer les instants t pour lesquels le solide (C) passe par sa position d'équilibre O. A quel instant t1 ce passage se fait pour la première fois ? 5)Tracer les courbes Ep =F(x2) et Ec=G(t) en précisant leurs valeurs particulières. Exercice 2 : On dispose d'un condensateur de capacité C=10 µF d'une bobine parfaite d'inductance L=0,1H et de résistance interne négligeable. 1)Pour charger le condensateur, on le soumet à une tension U0=10V délivrée par un générateur de courant continu.Le condensateur étant chargé, on le branche aux bornes de la bobine. Des oscillations électriques périodiques prennent naissance dans le circuit réalisé. a-Calculer la période propre T0 de l'oscillateur électrique utilisé. b-Etablir l'expression de la tension instantanée uC(t) aux bornes du condensateur. c-Donner l'expression de l'intensité instantanée i(t) du courant dans le circuit. Calculer sa valeur efficace. 2)a- Rappeler les expressions des énergies Ee et Em emmagasinées respectivement par le condensateur et la bobine, à une date t quelconque. b- Montrer que l'énergie totale E de l'oscillateur électrique utilisé est constante et donner sa valeur numérique. c- Représenter sur le même graphique les allures de courbes : Ee =f(t) ; Em =g(t) ; E=h(t) représentant les variations respectives de: Ee, Em et de E en fonction du temps. Commenter. |
|