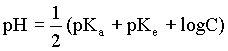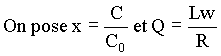Chimie: Les deux exercices 1 et 2 sont indépendants.
Toutes les solutions sont prises à 25°C.
Exercice 1:
On prélève un volume V0=10mL d'une solution d'acide éthanoique (ou
acétique) de concentration molaire C0=10-1mol.L-1, on
lui ajoute un volume V d'eau pure ; soit C la nouvelle concentration de la solution (S)
obtenue.
1)Etablir l'expression de C en fonction de C0 ; V0 et V.
2)On mesure le pH des solutions (S) ainsi obtenues pour différentes valeurs du volume V
d'eau ajoutée. On obtient les résultats consignés sur le tableau suivant :
| V(mL) |
0 |
10 |
20 |
40 |
60 |
90 |
150 |
| pH |
2,9 |
3,05 |
3,15 |
3,25 |
3,30 |
3,40 |
3,50 |
| C (mol.L-1) |
|
|
|
|
|
|
|
| -logC |
|
|
|
|
|
|
|
Avec log logarithme décimal.
a-Recopier et compléter le tableau précédent.
b-Représenter sur papier millimétré la courbe pH=f(-logC).
c-Etablir l'équation de la courbe obtenue.
3)a-Etablir l'expression du pKa de l'acide éthanoique en fonction du pH de la
solution
(S) et de sa concentration molaire C.
b- Déduire à partir de cette relation et de l'équation de la courbe précédente, la
valeur du pKa de l'acide éthanoique.
Exercice 2 :
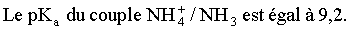
1)Montrer que le pH d'une solution aqueuse d'ammoniac de concentration molaire
C ( C étant de l'ordre de 10-3 à 10-1mol.L-1) est
donné par la relation:
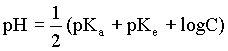
2)On prépare 500cm3 d'une solution aqueuse (S) d'ammoniac de pH=11,1.
a-Calculer la concentration molaire C de cette solution (S).
b-Quel volume d'eau faut-il ajouter à 500 cm3 de la solution (S) pour obtenir
une solution (S') telle que pH'=10,60 ?
c-Calculer et comparer les pourcentages de molécules d'ammoniac dissociées dans les
solutions (S) et (S'). Justifier le résultat de la comparaison.
Physique: Les trois exercices 1, 2 et 3 sont
indépendants.
Exercice 1 :
La lame métallique d'un vibreur est animée d'un mouvement rectiligne sinusoïdal
de fréquence N=100Hz et d'amplitude a=2mm. On fixe à l'extrémité S de cette lame une
corde très longue afin d'éviter la réflexion des ondes.
1)Etablir l'équation horaire du mouvement de S, en prenant pour origine des temps t=0s
celui du début du mouvement, S allant dans le sens négatif.
2)A la date t1=1,5.10-2s, le point M1 de la corde
d'abscisse x1=30cm entre à son tour en vibration. Calculer:
a-La célérité de propagation de l'onde le long de la corde.
b-La longueur d'onde 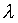 . .
3)a-Etablir l'équation horaire du mouvement de M1.
b-Chercher les instants pour lesquels les points S et M1 passent
pour la première
fois par leur élongation maximale.
c-Calculer les élongations de points S et M1 ainsi que leurs vitesses à la
date
t2=3,25.10-2s.
4)On considère deux points M2 et M3 de la corde d'abscisses
respectifs x2 et x3.
a-Exprimer le déphasage, entre ces deux points, en fonction de:
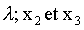
b-En déduire l'expression de la distance M2M3 entre ces deux points
pour qu'ils vibrent en opposition de phase. Calculer sa valeur minimale.
Exercice 2 :
On monte en série un résistor de résistance R=200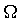 , une bobine d'inductance L=2H et de résistance propre
négligeable et un condensateur de capacité variable C. On alimente cet oscillateur par
un générateur imposant une tension alternative sinusoïdale de valeur efficace U=100V et
de fréquence f=800Hz. , une bobine d'inductance L=2H et de résistance propre
négligeable et un condensateur de capacité variable C. On alimente cet oscillateur par
un générateur imposant une tension alternative sinusoïdale de valeur efficace U=100V et
de fréquence f=800Hz.
On prendra 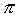 =25/8. =25/8.
1)Donner l'expression de l'intensité efficace I du courant dans l'oscillateur en fonction
des données du problème.
2)a-Exprimer, puis calculer, la valeur particulière C0 de la capacité qui
permet
d'obtenir un courant de valeur efficace maximale.
b-Calculer la valeur efficace I0 du courant qui traverse alors
l'oscillateur.
c-Calculer la tension efficace Uc0 aux bornes du condensateur.
3)La capacité est maintenant réglée à une valeur C différente de C0.
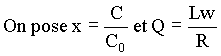
a-Exprimer la tension efficace UC aux bornes du condensateur en fonction de:
U ; R ; w ; C0 ; x.
b-Montrer que UC passe par un maximum pour une valeur particulière xm
de x et exprimer xm en fonction de R ; C0 et w.
c-Exprimer la valeur particulière Cm de la capacité correspondante en
fonction de
C0 et de Q.
Exercice 3 :
On néglige l'amortissement et toute réflexion aux bords de la cuve à ondes.
La surface d'une nappe d'eau contenue dans une cuve à ondes est excitée périodiquement
en deux points O1 et O2. Ceux-ci prennent, au cours du temps, les
élongations suivantes:
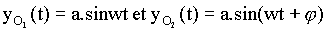
Où on désigne par:
*a : l'amplitude des excitations, a=2mm
*w : la pulsation des excitations

1)Quel est le phénomène observé à la surface de la nappe d'eau? Justifier.
2)On considère un point M du segment [O1O2] situé,
quand la surface de la nappe est au repos, à la distance d1 de O1
et à la distance d2 de O2.
a-Soit x'x l'axe orienté de O1 vers O2 et d'origine O, milieu du
segment [O1O2]. Exprimer d1 et d2 en fonction
de l'abscisse x du point M sur l'axe x'x et de la distance d séparant les points O1
et O2 lorsqu'ils sont au repos.
b-Soit 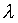 la longueur d'onde
à la surface de la nappe utilisée. la longueur d'onde
à la surface de la nappe utilisée.
Etablir l'équation horaire du mouvement du point M considéré.
c-En déduire que la phase initiale du mouvement d'un tel point ne peut prendre que deux
valeurs que l'on déterminera en fonction de:
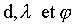
3)a-Déterminer les positions des points du segment [O1O2] vibrant
avec une
amplitude maximale en fonction de:

b-En déduire que ces points sont équidistants de:
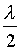
c-Sachant que l'on a 10 points d'amplitude maximale sur le segment [O1O2]
et que les deux points extrêmes sont séparés de 72mm, calculer 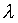 . .
4) Sachant que l'ensemble des points d'amplitude maximale présente une symétrie par
rapport à O, calculer les abscisses des deux points les plus proches de O. En déduire la
valeur du déphasage 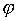 entre O1 et O2. entre O1 et O2.
|