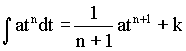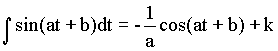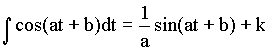Accueil Liens Fiches Laboratoires Formation Outils Evaluation Devoirs

Outils mathématiques
Première Deuxième Troisième Quatrième

Troisième année de l'enseignement secondaire
Sections: Math, Sciences expérimentales et Technique

Dérivée et primitive
invis.jpg (808 octets)
A-Dérivabilité:
I-Définition:f est une fonction numérique à variable réel, définie sur un intervalle .
On dit que: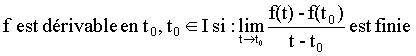

f est dérivable sur l'intervalle I si elle est dérivable en tout point de I.
La dérivée lorsqu'elle existe est notée: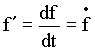

Exemple:
Soit à déterminer la dérivée par rapport à t de la fonction: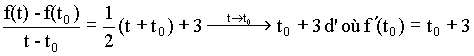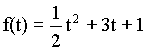



Généralisation:
Soit à déterminer la dérivée par rapport à t de la fonction: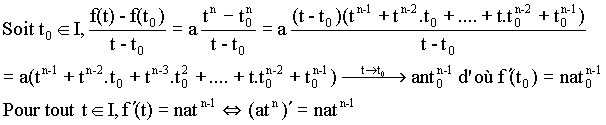


II-Propriétés de la dérivée:
Soient f et g deux fonctions dérivables et k une constante.
La somme (f+g) est dérivable et on a (f+g)'=f'+g'.
(kf) est dérivable et on a (kf)'=kf'.
Le produit (fg) est dérivable et on a (fg)'=f'g+fg'.
Soit f dérivable de I vers J, soit g dérivable sur J.
La composé gof est dérivable et on a: (gof)'=f'[g'of].
III-Dérivées usuelles:
(k)'=0.
(atn)'=natn-1.
(cost)'=-sint.
(sint)'=cost.
[cos(at+b)]'=-asin(at+b).
[sin(at+b)]'=acos(at+b).
B-Primitive d'une fonction:
I-Définition: f est une fonction continue sur un intervalle .
On appelle primitive de f la fonction F définie sur I telle que F'(t)=f(t) pour tout t appartenant à I.
Remarques:
Une fonction non continue n'admet pas de primitive.
Une fonction peut avoir plusieurs primitives égales à une constante près.
Si F et G deux fonctions primitives de alors G=F+k.
Il y a une seule primitive de f vérifiant F(t0)=0.
II-Primitives usuelles:


La primitive d'une fonction nulle est une constante.