Outils mathématiques:Première année de l'enseignement secondaire.

Outils mathématiques

Première année de l'enseignement secondaire

1)Aires et volumes de quelques formes géométriques:

Aires: S en m²

Volumes: V en m³

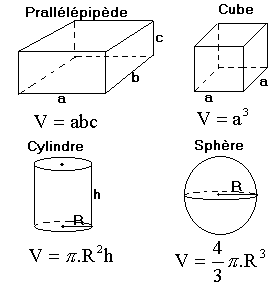2)Puissances:

	Quand on multiplie deux puissances d'un même nombre: les exposants s'ajoutent. aⁿ.a^m=a^n+m aⁿ.a^-m=a^n-m
	Quand on divise deux puissances d'un même nombre: les exposants se retranchent. aⁿ/a^m=a^n-m=1/a^m-n aⁿ/a^-m=a^n+m
	Puissances de 10: 1 suivi de n zéros peut s'écrire 10ⁿ 100=10² ; 100000=10⁵ ; 200=2.10² ; 279=2,79.10² 1 précédé de n zéros peut s'écrire 10^-n 0,01=10^-2 ; 0,00001=10^-5 ; 0,02=2.10^-2 ; 0,00015=1,5.10^-4

3)Proportions:
Une proportion est une égalité du type a/b=c/d.
a, b, c et d sont des réels non nuls.
a et d sont appelés les extrêmes et b et c les moyens.
Le produit de moyens est égal au produit des extrêmes alors ad=bc.

4)Bipoints:

	Le couple de points AB est appelé bipoint et noté (A,B). A est l'origine et B l'extrémité.
	Bipoints équipollents: Ils ont même sens même longueur et des directions parallèles.

Bipoint (A,B)

5)Vecteurs:

	Un vecteur est une classe d'équivalence de bipoints équipollents.
	On représente un vecteur par l'un quelconques de ses bipoints. Par exemple (M,N):

Vecteur

Un vecteur est défini par ses caractéristiques:
-Direction: celle de la droite MN.
-Sens : de M vers N.
-Norme:la distance des points M et N, c'est un nombre positif noté:

	Vecteur unitaire: Vecteur dont la norme est égale à 1.
	Valeur algébrique: Mesure de la projection d'un vecteur sur un axe. C'est un nombre positif ou négatif.

Multiplication d'un vecteur par un scalaire:

6)Fonctions:
a)Fonction linéaire: (Voir courbes 1 et 2).
Si la courbe y=f(x) est une droite qui passe par l'origine, la fonction f est dite linéaire. On peut écrire y=ax avec a: une constante représentant le coefficient directeur ou la pente de la droite.
On dit que y et x sont proportionnelles avec a le coefficient de proportionnalité.
On détermine la pente a en choisissant un seul point M₁(x₁,y₁) de la droite et on fait le rapport de son ordonnée y₁ par son abscisse x₁.
b)Fonction affine: (Voir courbes 3 et 4).
Si la courbe y=f(x) est une droite qui ne passe pas par l'origine, la fonction f est
dite affine. On peut écrire y=ax+b avec a et b deux constantes représentant respectivement le coefficient directeur de la droite et son ordonnée à l'origine.
On détermine la pente a en choisissant deux points M₁(x₁,y₁) et M₂(x₂,y₂) de la droite, l'un de ces deux points peut être l'origine O.
La constante b est donnée par l'intersection de la droite avec l'axe des ordonnées y.

Courbe 1(a>0)

Courbe 2(a<0)


Courbe 3(a>0)	Courbe 4(a<0)